
Le calcul d’annuité joue un rôle crucial dans de nombreux aspects de la planification financière, de l’évaluation des investissements à la structuration des prêts. Maîtriser cette compétence permet de prendre des décisions éclairées en matière de gestion financière personnelle et professionnelle. Que vous soyez un professionnel de la finance cherchant à affiner vos compétences ou un particulier souhaitant mieux comprendre vos options financières, la compréhension des principes fondamentaux du calcul d’annuité est essentielle.
Fondements mathématiques de l’annuité
Une annuité représente une série de paiements égaux effectués à intervalles réguliers sur une période déterminée. Le concept d’annuité repose sur la notion de valeur temporelle de l’argent , qui stipule que l’argent disponible aujourd’hui vaut plus que le même montant dans le futur en raison de son potentiel de gain. Cette idée est au cœur de nombreux calculs financiers, y compris celui des annuités.
La théorie mathématique derrière les annuités s’appuie sur des principes de progression géométrique et d’actualisation. Ces concepts permettent de déterminer la valeur actuelle ou future d’une série de paiements, en tenant compte du taux d’intérêt et de la durée. La complexité de ces calculs a conduit au développement de formules standardisées et d’outils spécialisés pour faciliter leur application pratique.
L’annuité est un outil financier puissant qui permet d’équilibrer les flux de trésorerie sur le long terme, offrant stabilité et prévisibilité dans la gestion financière.
Formule de base du calcul d’annuité

La formule fondamentale pour calculer la valeur actuelle d’une annuité ordinaire est :
VA = PMT * [(1 - (1 + r)^-n) / r]
Où :
- VA représente la valeur actuelle
- PMT est le montant de chaque paiement
- r est le taux d’intérêt par période
- n est le nombre total de périodes
Composantes de la formule : principal, taux d’intérêt et durée
Le principal est le montant initial emprunté ou investi. Le taux d’intérêt reflète le coût de l’emprunt ou le rendement de l’investissement, généralement exprimé en pourcentage annuel. La durée correspond au nombre de périodes sur lesquelles les paiements sont effectués. Ces trois éléments sont interdépendants et influencent directement le montant de l’annuité.
Par exemple, pour un prêt de 100 000 € sur 20 ans à un taux d’intérêt annuel de 3%, l’annuité serait calculée comme suit :
Annuité = 100 000 * (0,03 * (1 + 0,03)^20) / ((1 + 0,03)^20 - 1) ≈ 6 721,57 €
Utilisation de la fonction valeur actuelle (VA) dans excel
Excel offre une fonction intégrée pour calculer les annuités : la fonction VA (Valeur Actuelle). Cette fonction simplifie grandement les calculs complexes d’annuités. Pour l’utiliser, il suffit d’entrer les paramètres dans la formule suivante :
=VA(taux; nper; pmt; [vf]; [type])
Où :
- taux : taux d’intérêt par période
- nper : nombre total de périodes de paiement
- pmt : paiement effectué à chaque période
- vf (optionnel) : valeur future souhaitée
- type (optionnel) : 0 pour paiements en fin de période, 1 pour paiements en début de période
Adaptation de la formule pour les annuités différées
Les annuités différées sont des annuités dont les paiements ne commencent qu’après une certaine période. Pour calculer la valeur actuelle d’une annuité différée, on modifie la formule de base en ajoutant un facteur d’actualisation pour la période de différé :
VA_différée = VA * (1 + r)^-d
Où d représente le nombre de périodes de différé. Cette adaptation est particulièrement utile dans le calcul de certains produits d’assurance-vie ou de retraite différée.
Calcul de l’annuité avec la méthode de Newton-Raphson
Pour des calculs plus complexes, notamment lorsqu’on cherche à déterminer le taux d’intérêt d’une annuité connaissant les autres paramètres, la méthode de Newton-Raphson peut être employée. Cette méthode itérative permet d’approximer la solution d’équations non linéaires avec une grande précision.
L’application de cette méthode nécessite généralement l’utilisation d’outils de calcul avancés ou de programmation, mais elle offre une flexibilité et une précision accrues dans les situations où les formules standard ne suffisent pas.
Types d’annuités et leur impact sur le calcul
La diversité des types d’annuités reflète la complexité des besoins financiers modernes. Chaque type d’annuité nécessite une approche de calcul légèrement différente, adaptée à ses caractéristiques spécifiques.
Annuités ordinaires vs annuités dues
La principale différence entre ces deux types d’annuités réside dans le moment où les paiements sont effectués. Dans une annuité ordinaire , les paiements sont réalisés à la fin de chaque période, tandis que dans une annuité due , ils sont effectués au début. Cette distinction affecte le calcul de la valeur actuelle et future de l’annuité.
Pour convertir une annuité ordinaire en annuité due, on multiplie la valeur de l’annuité ordinaire par (1 + r), où r est le taux d’intérêt par période. Cette ajustement reflète le fait que les paiements dans une annuité due génèrent des intérêts sur une période supplémentaire.
Annuités certaines et annuités contingentes
Les annuités certaines ont une durée fixe et garantie, tandis que les annuités contingentes dépendent d’un événement incertain, souvent lié à la durée de vie d’une personne. Le calcul des annuités contingentes intègre des éléments de probabilité et d’espérance de vie, rendant leur évaluation plus complexe.
Pour les annuités contingentes, on utilise souvent des tables de mortalité en conjonction avec les formules d’annuités standard pour estimer la valeur actuarielle des paiements futurs.
Annuités temporaires et annuités perpétuelles
Les annuités temporaires ont une durée limitée, tandis que les annuités perpétuelles , théoriquement, continuent indéfiniment. Le calcul d’une annuité perpétuelle est simplifié car sa valeur actuelle est simplement le paiement annuel divisé par le taux d’intérêt :
VA_perpétuelle = PMT / r
Cette formule découle de la limite mathématique de la formule d’annuité standard lorsque le nombre de périodes tend vers l’infini.
La compréhension des différents types d’annuités est cruciale pour choisir le produit financier le plus adapté à des objectifs spécifiques, qu’il s’agisse de planification de retraite, d’investissement ou de gestion de dette.
Outils et logiciels pour le calcul d’annuités
L’évolution technologique a grandement facilité le calcul d’annuités, offrant une variété d’outils adaptés à différents niveaux d’expertise et besoins spécifiques.
Calculatrices financières texas instruments BA II plus
La Texas Instruments BA II Plus est une calculatrice financière prisée des professionnels pour sa capacité à effectuer rapidement des calculs d’annuités complexes. Elle offre des fonctions préprogrammées pour calculer les valeurs actuelles et futures, les paiements, et même le nombre de périodes ou le taux d’intérêt d’une annuité.
Pour calculer une annuité sur la BA II Plus :
- Appuyez sur la touche [2nd] [CLR TVM] pour effacer la mémoire TVM
- Entrez les valeurs connues (N pour le nombre de périodes, I/Y pour le taux d’intérêt, PV pour la valeur actuelle si connue)
- Appuyez sur la touche correspondant à la valeur que vous cherchez (PMT pour le paiement, FV pour la valeur future)
Modules d’annuités dans python avec NumPy et SciPy
Python, avec ses bibliothèques NumPy et SciPy, offre des outils puissants pour les calculs financiers avancés, y compris les annuités. Ces modules permettent non seulement d’effectuer des calculs standard, mais aussi de créer des modèles financiers complexes et d’automatiser des séries de calculs.
Voici un exemple simple de calcul d’annuité utilisant NumPy :
import numpy as nppv = 100000 # Valeur actueller = 0.05 # Taux d'intérêt annueln = 20 # Nombre d'annéespmt = np.pmt(r, n, pv)print(f"Le paiement annuel est de : {-pmt:.2f}")
Ce code calcule le paiement annuel nécessaire pour rembourser un prêt de 100 000 € sur 20 ans à un taux de 5%.
Fonctionnalités avancées de calcul d’annuités dans R
R, un langage de programmation statistique, offre également des fonctionnalités robustes pour le calcul d’annuités à travers des packages spécialisés comme FinCal ou financial . Ces packages permettent non seulement d’effectuer des calculs d’annuités standard mais aussi d’analyser des scénarios complexes et de visualiser les résultats.
Un exemple d’utilisation du package FinCal pour calculer la valeur actuelle d’une annuité :
library(FinCal)pv <- pv(r = 0.05, n = 20, pmt = -7000, fv = 0, type = 0)print(paste("La valeur actuelle est de :", round(pv, 2)))
Ce code calcule la valeur actuelle d’une annuité de 7 000 € par an pendant 20 ans à un taux de 5%.
Applications pratiques du calcul d’annuités
Le calcul d’annuités trouve de nombreuses applications dans le monde financier, de la planification personnelle aux stratégies d’entreprise complexes.
Planification de retraite avec le modèle d’annuités de yaari
Le modèle d’annuités de Yaari, développé par l’économiste Menahem Yaari, propose une approche théorique pour optimiser la consommation et l’épargne tout au long de la vie d’un individu. Ce modèle utilise le concept d’annuités pour démontrer comment une personne peut maximiser son utilité en convertissant une partie de son patrimoine en flux de revenus réguliers.
L’application de ce modèle dans la planification de retraite implique de calculer le montant optimal à convertir en annuité pour assurer un revenu stable tout en maintenant une flexibilité financière. Cela nécessite de prendre en compte des facteurs tels que l’espérance de vie, les taux d’intérêt prévus et les préférences personnelles en matière de risque.
Structuration de prêts immobiliers et calcul des mensualités
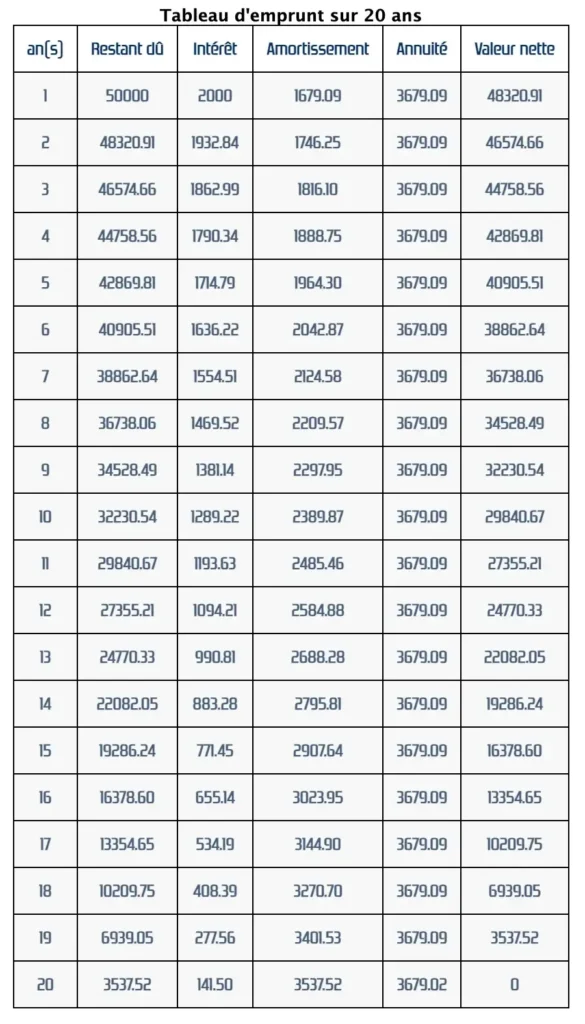
Dans le domaine des prêts immobiliers, le calcul d’annuités est essentiel pour déterminer les mensualités et structurer le remboursement. Les banques utilisent ces calculs pour établir des tableaux d’amortissement, montrant comment le capital est remboursé au fil du temps.
Par exemple, pour un prêt immobilier de 250 000 € sur 25 ans à un taux fixe de 2,5%, le calcul de l’annuité mensuelle serait :
Mensualité = 250000 * (0,025/12) / (1 - (1 + 0,025/12)^-300) ≈ 1 121,54 €
Ce calcul permet aux emprunteurs de comprendre leur engagement financier et aux prêteurs d’évaluer le risque et la rentabilité du prêt.
Évaluation des contrats d’assurance-vie basés sur les annuités
Les contrats d’assurance-vie utilisant des annuités offrent une garantie de revenu pour une période déterminée ou pour la vie. L’évaluation de ces contrats nécessite des calculs d’annuités complexes qui prennent en compte l’espérance de vie, les taux d’intérêt garantis et les options de paiement.
Les actuaires utilisent des modèles sophistiqués basés sur les principes d’annuités pour déterminer la prime à payer pour un certain niveau de couverture ou pour calculer le montant des versements périodiques qu’un assuré peut s’attendre à recevoir.
Par exemple, pour un contrat d’assurance-vie avec une prime unique de 100 000 € et une espérance de versements sur 20 ans, le calcul de l’annuité pourrait être :
Annuité = 100 000 * (1 + 0,03)^20 / ((1 + 0,03)^20 - 1) ≈ 6 721,57 €
Ce calcul suppose un taux d’intérêt garanti de 3% et ne tient pas compte des facteurs de mortalité. En pratique, les actuaires ajusteraient ce calcul en fonction des tables de mortalité et d’autres facteurs de risque spécifiques.
| Type d’application | Facteurs clés | Complexité du calcul |
|---|---|---|
| Planification de retraite | Espérance de vie, tolérance au risque | Moyenne à élevée |
| Prêts immobiliers | Taux d’intérêt, durée du prêt | Faible à moyenne |
| Assurance-vie | Tables de mortalité, options de paiement | Élevée |
En conclusion, le calcul d’annuités est un outil polyvalent et puissant dans le monde de la finance. Que ce soit pour planifier sa retraite, structurer un prêt immobilier ou évaluer un contrat d’assurance-vie, la maîtrise de ces calculs permet de prendre des décisions financières éclairées. Avec l’évolution constante des outils technologiques, ces calculs deviennent de plus en plus accessibles, permettant à chacun de mieux comprendre et gérer ses finances personnelles.
Cependant, il est important de rappeler que bien que ces calculs fournissent des indications précieuses, ils ne sont qu’un aspect de la prise de décision financière. Des facteurs tels que l’inflation, les changements de situation personnelle ou les fluctuations du marché doivent également être pris en compte pour une planification financière globale et robuste.